LEC2

• Introduction to 1D kinematics.

• Definitions of positional, motional parameters in one dimension.

• Explored graphs of parameters.

• Kinematics in 1D:

  • Straight line motion. We consider only the forwards and backwards motion.
  • We assume the object is a rigid particle that experiences change uniformly throughout it’s body without any stretching, rotation.
  • Reference frame in 1D is the origin ⇒ $x\in (-\infty ,\infty )$

Definitions

Displacement

A change in the x-coordinate of our particle / change in position.

$$\Delta x=x_2-x_1$$

Average Velocity

$$V_{\text{avg-x}}=\frac{\Delta x}{\Delta t}$$

X-T graph

In a position-time graph, visualize the motion of particle as if it is moving up and down the y-axis. The curve traced by the graph is NOT the actual path of the particle. 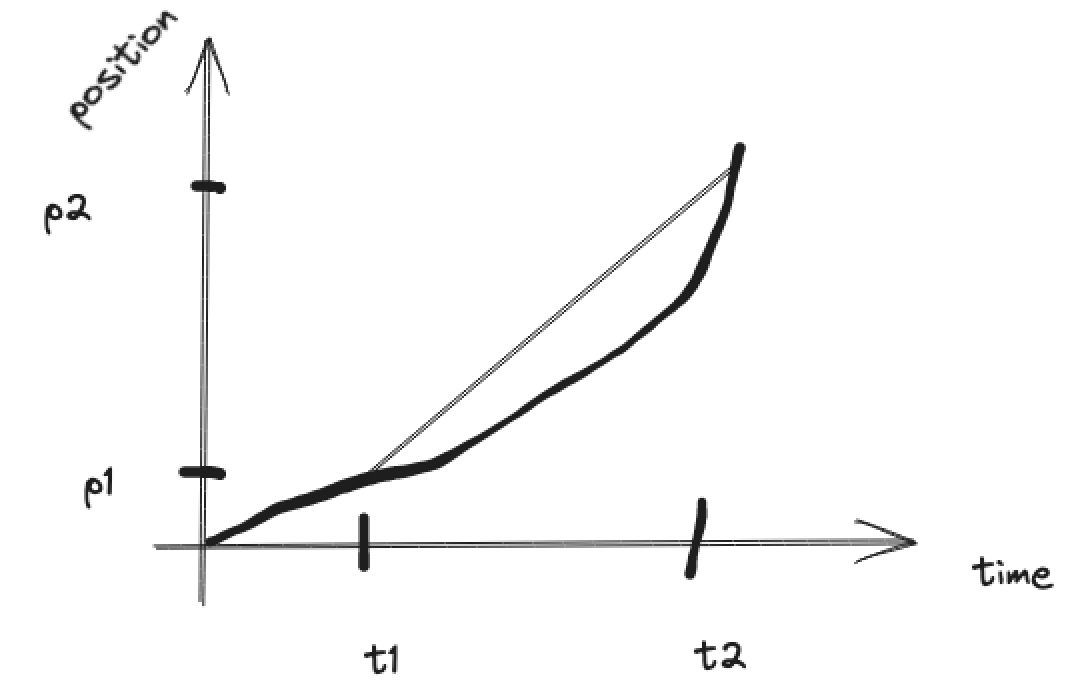Average velocity in an interval is given by the slope of the line connecting the two intervals.

Average Speed

NOT the same as avg. velocity. $\text{Avg. Speed}=\frac{\text{distance}}{\text{time}}$

Instantaneous Velocity

Velocity of a particular at a particular instant of time.

Avg. velocity is calculated over an interval of time. If me make our interval smaller and smaller until in approaches zero, we have an interval so small it is an instant of time.

$$V_x=\underset{\Delta t\to 0}{\lim }\frac{\Delta x}{\Delta t}=\frac{dx}{dt}$$

Velocity is the first derivate of position ⇒ the slope of an x-t graph tells us the nature of velocity (positive, negative)

Instantaneous Speed

Absolute value of velocity. $\text{Inst. Speed}=|v_x|$

The two definitions are very close because the interval of time is so small that there is no different between displacement and distance.

Average Acceleration

Rate of change of velocity over an interval of time.

$$a_{av-x}=\frac{\Delta v_x}{\Delta t}$$

Acceleration

Acceleration of particle at a particular instant of time.

Similar to velocity, as our time interval becomes smaller and approaches zero, it becomes an instant.

$$a_x=\underset{\Delta t\to 0}{\lim }\frac{\Delta v}{\Delta t}=\frac{dv}{dt}$$

Since acceleration is the second derivative of position, the curvature of an x-t graph tells us the nature of acceleration.

• A curvy graph implies the line is not a straight line ⇒ slope is changing ⇒ velocity is changing.
• Downward curve ⇒ slope is decreasing ⇒ velocity is decreasing ⇒ de-acceleration.
• Upward curve ⇒ slope is increasing ⇒ velocity is increasing ⇒ acceleration.

[!Curve is not slope] Curvature is not the same as slope Curvature is the change of slope.

3b1b on higher order derivatives