Steps to solve an inequality

• Basic inequalities like $x+10<0$ can be solved just by common sense.
• But longer polynomial inequalities, especially those involving multiplication, require us to consider the inequality in “cases”.

$$(x-5)(x-3)>0$$

Case 1: both brackets evaluate to positive.

$$\begin{array}{r}x-5>0\\ x>5\\ \\ x-3>0\\ x>3\\ \\ ⟹x\in (5,\infty )\end{array}$$

Case 2: both brackets evaluate to negative.

$$\begin{array}{r}x-5<0\\ x<5\\ \\ x-3<0\\ x<3\\ \\ ⟹x\in (-\infty ,3)\end{array}$$

Considering both cases:

$$x\in (-\infty ,3)\cup (5,\infty )$$

• It’s tedious with just two cases. So instead of solving each case separately, we can use this thing called wavy curve method and a couple of shortcuts to avoid solving each case.

Steps:

1. Factorize the inequality.
2. Identify the critical points–points around which the sign of the expression changes.
3. Plotting these critical points on a number line will divide the line into regions.

Now, normally we would consider each of these “regions” as a case and check if the numbers in the interval satisfy our inequality. But, instead of solving these cases, we can convert the expression into a familiar format such that we can find the sign of the interval without actually solving the expression.

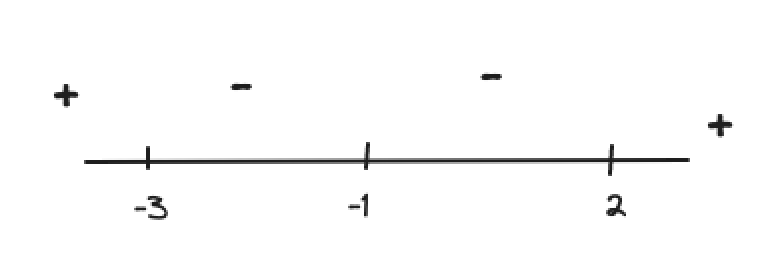
4. Find the sign of our inequality in each of these regions.
5. Ensure that, in each of the factors, $(x-n),(c-x)$, our $x$ is always positive.

$$\begin{array}{r}(x-n)(c-x)>0\\ -(x-n)(x-c)>0\\ (x-n)(x-c)<0\end{array}$$

5. Now starting from the right-most interval, we can start annotating our intervals with their signs.
   1. The right-most interval is always positive.
   2. When we cross over into the next interval, our sign may flip.
   3. Sign flips if the critical point’s bracket’s power is odd.
   4. Eg: $(x-5{)}^2(x+1{)}^3>0$. Here critical point 5 has an even power, so when we cross it, the sign will not flip. But while crossing -1, our sign will flip.

$$\begin{array}{r}\frac{(x+1{)}^4(x+3)}{(x-2{)}^3(x^2+1)}\ge 0\end{array}$$

Here $(x^2+1)$ has been multiplied with 0 (hence ignored) as the term will always be positive.

$$x\in (-\infty ,-3]\cup (2,\infty )\cup \{1\}$$