Circular Motion

Object goes around circle at a constant speed.
- Constant speed not velocity as velocity cannot be constant in a circle.
- The direction is always changing ⇒ velocity is always changing.
- Here the magnitude of velocity, i.e. speed, stays constant.
Velocity is always tangential here.
- Change in velocity is toward the inside.
- Since there is no change in tangential velocity, there is no tangential acceleration.
- The only acceleration is to keep the object in the circle–centripetal acceleration.
- When we look at the change in velocity (basically the change in direction here), and make the time interval very small, hence making the angle traversed very small, our $Δ v$ is almost perpendicular to both initial and final velocity. Since acceleration is $Δ v / t$ , acceleration is also perpendicular to velocity. Toward the center.

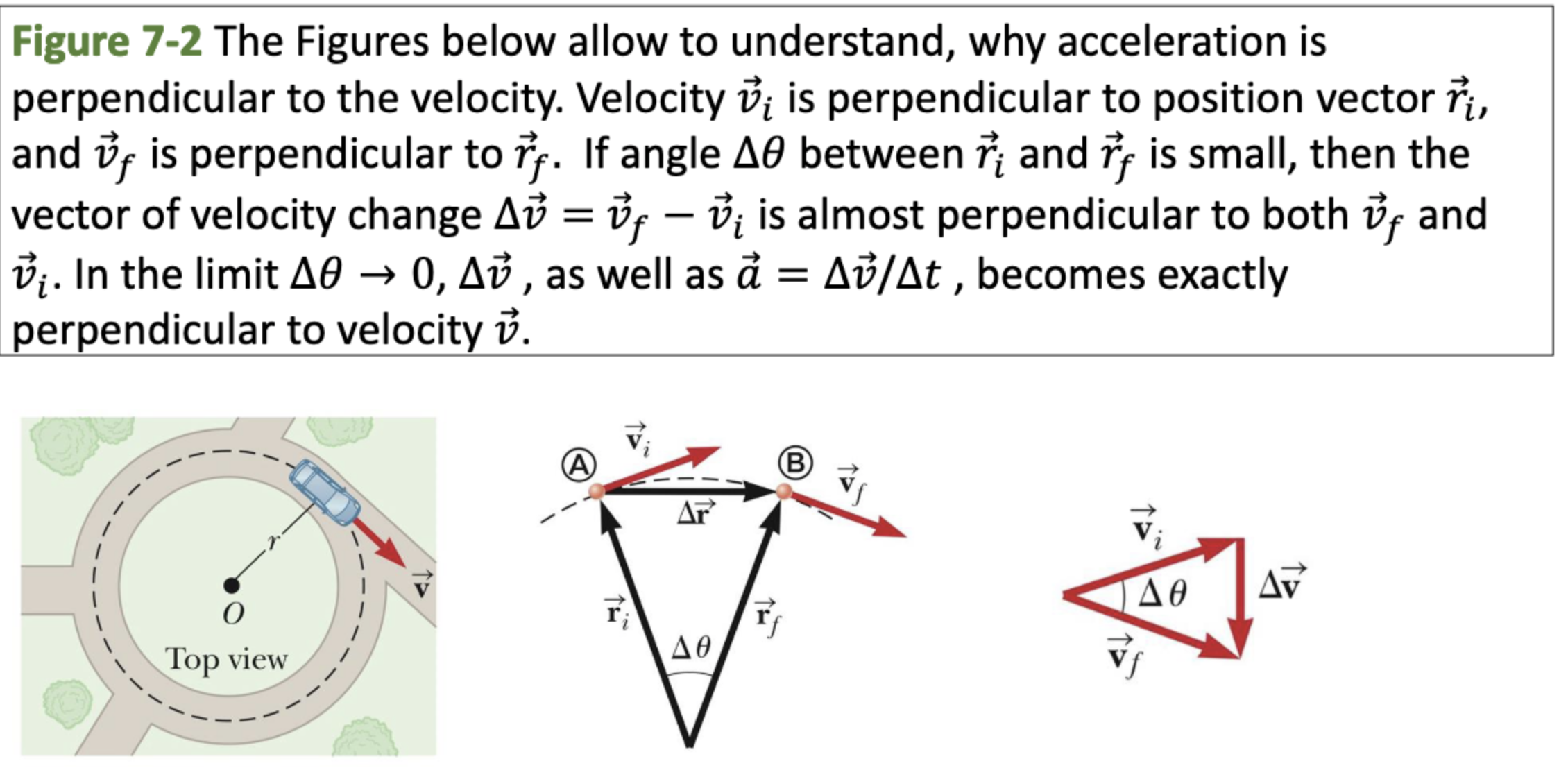
Centripetal Acceleration

a = \frac{v ^{2}}{r}

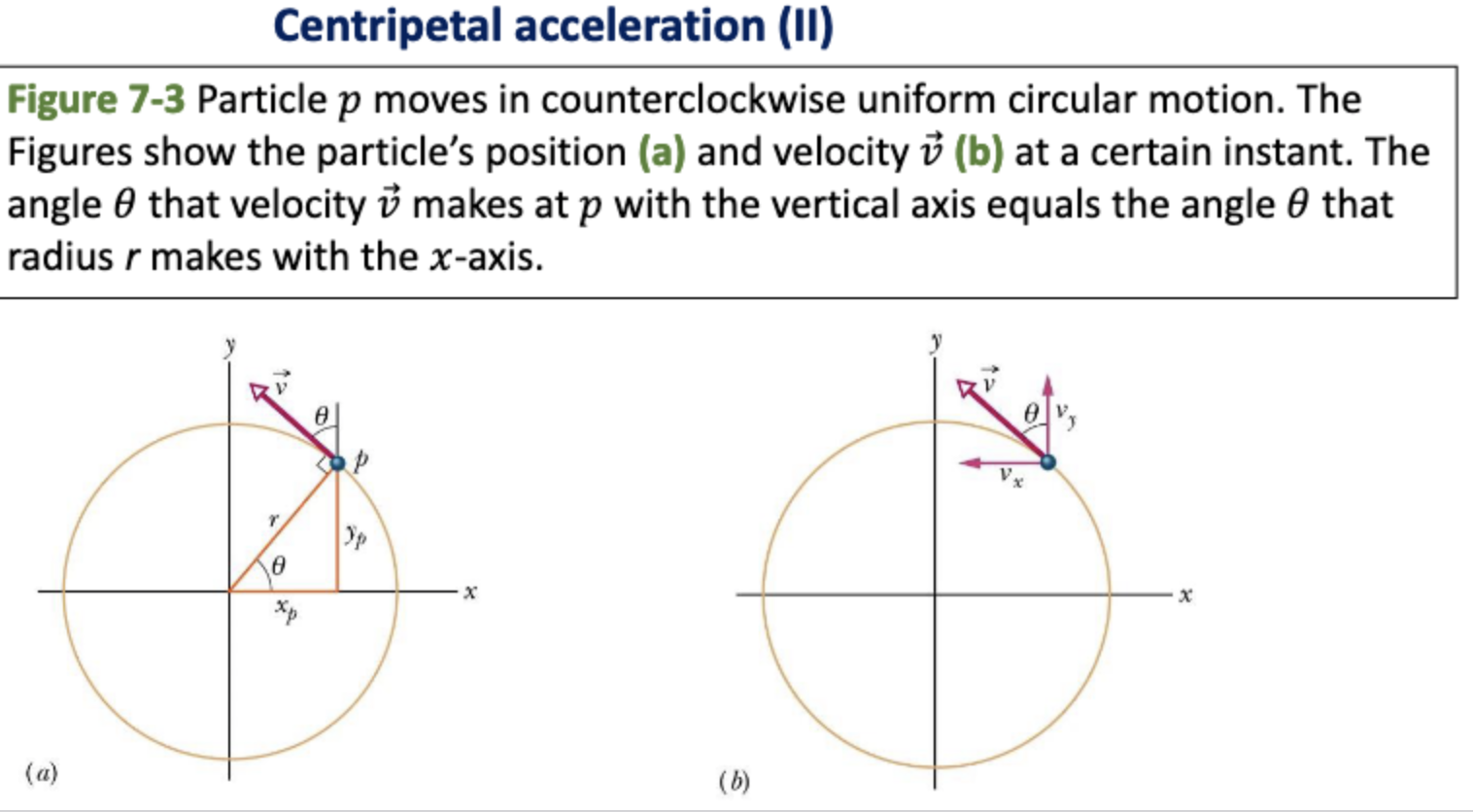
Particle moves around a circle at $v$ .
- $v$ is perpendicular to $r$ .
- $r$ is at angle $θ$ to the x-axis.
- By geometry, $θ$ is the angle between $v$ and the vertical.

v_{x} = - v sin θ v_{y} = v cos θ v = (- v sin θ) \hat{i} + (v cos θ) \hat{j} sin θ = y / r cos θ = x / r v = (- v \frac{y}{r}) \hat{i} + (v \frac{x}{r}) \hat{j} a = (- \frac{v}{r}) (\frac{d y}{d t}) \hat{i} + (\frac{v}{r}) (\frac{d x}{d t}) \hat{j} = (- \frac{v}{r}) (v_{y}) \hat{i} + (\frac{v}{r}) (v_{x}) \hat{j} = (- \frac{v}{r}) (v cos θ) \hat{i} + (\frac{v}{r}) (- v sin θ) \hat{j} a = - \frac{v ^{2} cos θ}{r} \hat{i} - \frac{v ^{2} sin θ}{r} \hat{j} ∣ a ∣ = \frac{v ^{2}}{r}

Angle $ϕ$ acceleration makes with x-axis:

tan ϕ = \frac{a _{y}}{a _{x}} = \frac{\frac{- v ^{2} s i n θ}{r}}{\frac{- v ^{2} c o s θ}{r}} tan ϕ = tan θ

T = \frac{2 π r}{v}

(speed = distance / time ⇒ time = dist / speed)

v = \frac{2 π r}{T} ω = \frac{2 π}{T} v = ω r a = ω^{2} r = \frac{v ^{2}}{r}

a = a_{r} + a_{t}