Scaler Equation of a Plane

$$\overrightarrow{PQ}\cdot \hat{n}=0$$

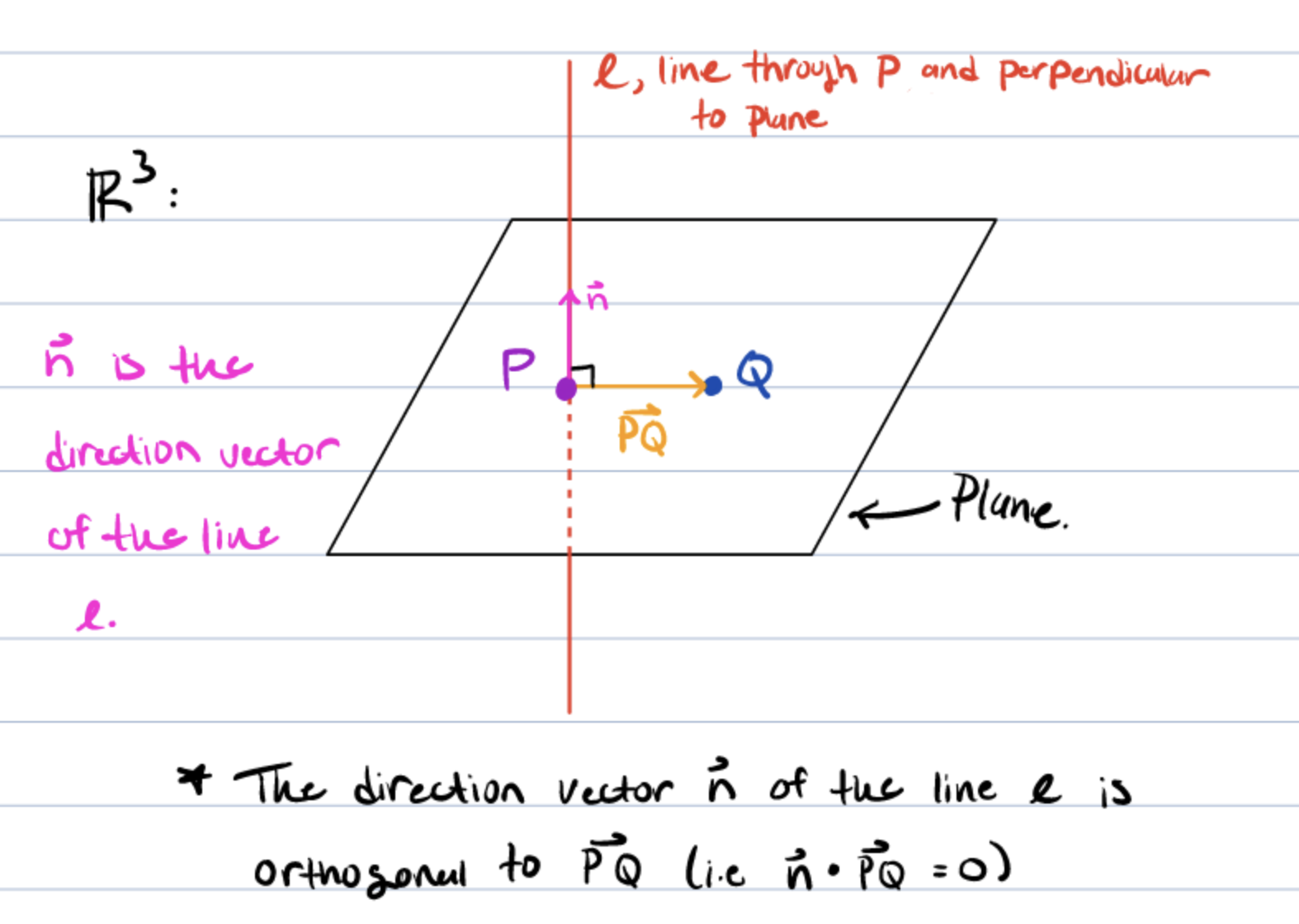
• We have a plane in $R^3$.

• Take a point $P$ on this plane.

• There is a unique line passing through this point.

  • This line is (by definition) perpendicular to the surface of the plane.
  • We call this the normal vector $\hat{n}$.

• Now take any arbitrary point on the plane: $Q$.

• For $Q$ to lie on the plane it must satisfy the following:

  • $PQ$, the vector between $P$ and $Q$, must be perpendicular to $\hat{n}$, the normal vector.

• Since $\vec{n}$ is perpendicular to the surface of the plane, it is perpendicular to every vector lying on the plane.

• If any point fails the perpendicularity property, it does not lie on the plane.

$$\overrightarrow{PQ}\cdot \hat{n}=0$$

• Any two normal vectors of a plane are parallel ⇒ they are unique except for a nonzero scalar multiple.

Expansion of the Equation

$$\begin{array}{r}\hat{n}\cdot \overrightarrow{PQ}=0\\ \hat{n}\cdot (\overrightarrow{OQ}-\overrightarrow{OP})=0\\ \hat{n}\cdot \overrightarrow{OQ}-\hat{n}\cdot \overrightarrow{OP}=0\\ \hat{n}\cdot \overrightarrow{OQ}=\hat{n}\cdot \overrightarrow{OP}\\ \left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]\cdot \left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\\ n_1{x}_1+n_2{x}_2+n_3{x}_3=n_1{p}_1+n_2{p}_2+n_3{p}_3\\ n_1{x}_1+n_2{x}_2+n_3{x}_3=d\\ \\ \\ ⟹d=\hat{n}\cdot \vec{x}\end{array}$$

Why Scalar Equation

• Easier to check if point is on the plane with this equation.
• Easier to tell the normal vector of a plane (similar to how we can easily tell the direction vector of a line).
  • Two lines are parallel if their direction vectors are parallel.
  • Two planes are parallel if their normal vectors are parallel.

Hyperplanes

$$d={\hat{a}}_n\cdot {\vec{x}}_n$$